Разное by alexxlab

Методика евгения чаплыгина: в чем ее уникальность и интерес?

в чем ее уникальность и интерес?

Здравствуйте, дорогие родители!

Многие родители придерживаются стратегии о раннем развитии, что ребенок должен получить максимум информации в свои первые годы жизни.

Я отчасти тоже разделяю это мнение, но стараюсь слишком не перегружать информацией своего двухлетнего сына, если он не хочет заниматься, я не настаиваю.

Многие методики у всех на устах, такая как Монтессори или Г. Домана, к примеру. Но так же, не менее популярна и методика Евгения Чаплыгина. В чем ее уникальность и вызванный интерес?

Содержание

  1. Об авторе и его методике
  2. Динамические кубики
  3. Домино
  4. Для какого возраста
  5. Минусы и плюсы методики

Об авторе и его методике

Автором данной методики является российский педагог и тренер Евгений Васильевич Чаплыгин. Проработал с детьми 35 лет в детской спортивной школе. А так же многодетный отец троих детей, в данное время еще и внуков.

В его семье много читали и любили читать. И детям в том числе было прочитано не одна сотня различных книг и книжечек.

Для обучения своего младшего сына Евгений Васильевич встретил на полках магазина «Азбуку Льва Толстого». Азбука была необычной и что удивляло больше всего: алфавит был размещен на самой последней странице.

Лев Толстой применял в своем обучении детей склады, и настоятельно рекомендовал учить буквы только после того, как ребенок уже научился читать.

Так этот метод схож с методом Зайцева, именно с него все и началось. Чаплыгину было понятно и приемлемо такое обучение по складам, которое позиционировал Зайцев, ведь своего младшего сына он тоже учил чтению по складам.

Но Чаплыгин счел методику слишком сложной. Он хотел максимально упростить процесс обучения как для детей, так и для родителей и конечно, чтобы детям было интересно заниматься.

Появилась идея разработки динамических кубиков Чаплыгина. Было подобрано несметное количество сочетаний, проделана трудоемкая работа.

Два кубика, соединенные вместе: гласная и согласная, при вращении получаем новый звук и другое слово Да-Ду-Де.

Ребенку понятно, он улавливает эту закономерность и САМОСТОЯТЕЛЬНО обучается дальше, и не нужно ничего лишнего объяснять, чем мы только ему мешаем. В этом и есть особенность метода.

Тогда Евгений Васильевич всерьез задумывается о внедрении своего продукта в мир. Совместно со студией образовательных инноваций «Развивающие технологии» внедряет свою методику по сей день.

Все пособия запатентованы, имеют золотые награды и дипломы.

Данная методика включает себя волшебные кубики для чтения и домино для обучению счета и получила название «читаю и считаю легко».

Как говорит автор, чтение — это легко и просто! Мы — взрослые, все усложняем и только путаем и захламляем голову ребенка ненужной информацией, отсюда и потерянное время и нежелание ребенка учиться.

Занимаясь по таким кубикам можно за считанные дни обучить ребенка чтению. Даже на коробке указано, что это произойдет за три дня.

Но вы должны понимать, что все зависит от первоначального уровня знаний вашего малыша: если он знаком с буквами, может и за три дня, а если он не имеет понятия про них, тогда времени уйдет однозначно больше.

Не торопитесь сами и не торопите ребенка, путь он вдоволь наиграется.

Динамические кубики

 

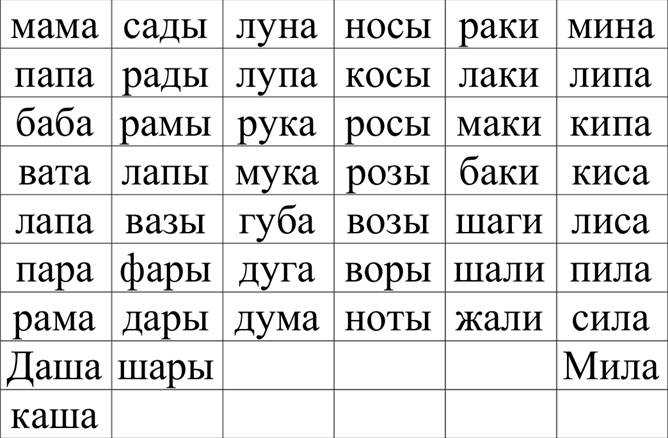
В комплект для обучения чтению входит: 10 обычных кубиков, на сторонах которых написаны буквы и 10 динамических кубиков, которые соединены между собой платформами на которых они могут вращаться в любую сторону, таким образом образуя слог.

Данный вид конструкции запатентован и является уникальной разработкой автора. Ребенок крутит кубик и для него это игровой процесс.

Автор убежден, что посредством данной методики ребенок легче и быстрее понимает, как из букв образуются слова. Здесь задействовано несколько факторов: это и зрительное восприятие и тактильный эффект. Ребенок держит и вертит в руках кубик — работает мелкая моторика, тут же и произносит данный слог или склад.

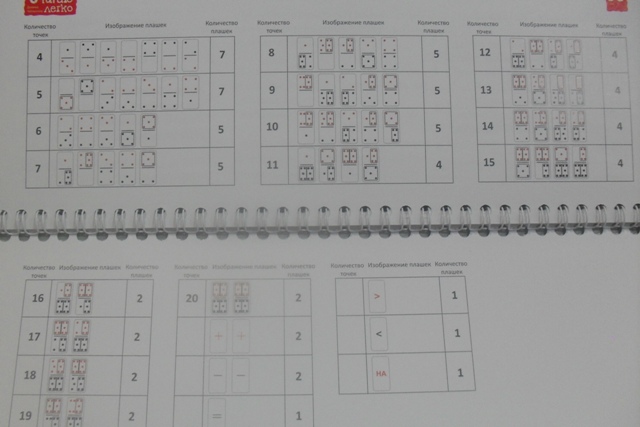
Домино

Это еще одна из разработок, на этот раз для обучению детей цифрам и счету. Домино это непростое, бамбуковое и содержит в наборе аж 90 плашек с цифрами — точками и плашки с арифметическими знаками.

Казалось бы что выглядит, как обычное домино, что может заинтересовать ребенка? — точки?

А вот и не угадали, как показывает практика, дети охотно играют в Чаплыгинское домино. Главное правило здесь: только игра, никаких теорий и занудных тетрадей, все операции с цифрами можно провести в этом домино.

За 8 несложных шагов, описанных в книжке -шпаргалке, которая прилагается к набору, ваш ребенок освоит цифры, счет и математические действия.

Играя в подобные игры у ребенка активно развивается мышление, воображение, развивается память, внимание и интеллект. Он учится самостоятельно анализировать, делать выводы, принимать решения.

Для какого возраста

 

Автором рекомендован возраст от трех лет. Мы купили в два года. Предложите ребенку, все детки разные — кого-то сразу заинтересует, кому-то понадобится время. Нам лично первое время очень нравилось просто крутить кубик, как игрушку и перевозить их на большом игрушечном камазе.

Минусы и плюсы методики
  • Одним из неприятных факторов могу указать опять же на ценовую категорию. Когда я впервые заинтересовалась данными кубиками была просто убита ценой комплекта. Это было мое первое впечатление. Но потом, если сравнивать с другими развивающими методиками, то они тоже в этом же диапазоне цен. Не каждый родитель готов выложить такую сумму за набор.

 

  • Ребенок может как самостоятельно работать с кубиками или домино, так и в компании.

 

  • Домино и кубики можно использовать и не по назначению, например,  в качестве стройматериала, которого постоянно не хватает, чтобы заполонить детскую.

 

  • Гласные отмечены красным цветом, а согласные черным, чтобы сразу ребенок понимал и визуально запоминал какая буква гласная, какая согласная. Работает память как визуальная, так и слуховая, постоянно проговаривайте слова и слоги.

 

  • Ребенок сразу все запоминает правильно, ему не придется переучиваться или что-то доучивать потом.

 

  • Небольшой по габаритам набор не займет много места в детской комнате и полностью готов после покупки к эксплуатации и освоению: ничего не нужно дополнительно вырезать или клеить.

Читайте и считайте, играйте и улыбайтесь!

Всего доброго, до новых встреч!

С уважением, Юлия Полонская

ОбучариУм. МЕТОДИКИ ЧАПЛЫГИНА

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

  • Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

  • Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
  • Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
  • Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
  • Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

  • В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
  • В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

С. А. Чаплыгин, “К теории движения неголономных систем.

Теорема о редуцирующих множителях”, Regul. Хаотическая динамика, 13:4 (2008), 369–376
Общая информация
Последний выпуск
Архив
Импакт-фактор

Поисковые документы
Поиск ссылок

RSS
Последний выпуск
Текущие выпуски
Выпуски архива
Что такое RSS






Личный кабинет:
Логин:
Пароль:
Сохранить пароль
Введите
Забыли пароль?
Регистр

Регулярная и хаотическая динамика, 2008 г. , том 13, выпуск 4, страницы 369.–376
DOI: https://doi.org/10.1134/S1560354708040102 (Ми rcd584)		  
Эта статья цитируется в
50 научных статьях (всего в 51 статьях)

Неголономная механика

К теории движения неголономных систем. Теорема о уменьшающем множителе

С. А. Чаплыгин

Императорское Московское техническое училище, Россия

DOI: https://doi.org/10.1134/S1560354708040102

Реферат: Классическая статья С.А. Чаплыгина представляет собой часть его исследований по неголономной механике. В этой статье Чаплыгин предлагает общий метод интегрирования уравнений движения для неголономных систем, который он сам назвал «методом редукционных множителей». Метод иллюстрируется двумя конкретными задачами неголономной механики. Эта работа оказала значительное влияние на дальнейшее развитие русского неголономного сообщества. С помощью теории приводящих множителей Чаплыгина были решены уравнения для целого ряда неголономных систем (такие системы известны как системы Чаплыгина). Впервые опубликованная около ста лет назад, эта работа не утратила своего научного значения и, надеемся, будет оценена по достоинству англоязычным миром. Настоящая публикация дополняет серию переводов научного наследия Чаплыгиных в формате RCD. В 2002 г. мы опубликовали две его работы (обе цитируются здесь) в специальном выпуске, посвященном неголономной механике (ОКД, т. 7, № 2). Эти переводы, наряду с переводами двух других его работ по гидродинамике (ОКД, т. 12, № 1, 2), вызвали значительный интерес и широко цитируются современными исследователями.

Ключевые слова: неголономные системы, теорема о редукционном множителе, интегрирование

Библиографические базы данных:

Тип документа: Персоналия

MSC: 37J60

Язык: Английский

Цитата: С. А. Чаплыгин, “К теории движения неголономных систем. Теорема о редуцирующих множителях”, Regul. Хаотическая динамика, 13:4 (2008), 369–376

Цитирование в формате AMSBIB

\RBibitem{Cha08}
\by С.~А.~Чаплыгин
\paper К теории движения неголономных систем. Теорема о редуцирующих множителях
\jour Regul. Хаотичный дин.
\год 2008
\том 13
\выпуск 4
\страниц 369--376
\mathnet{http://mi.mathnet.ru/rcd584}
\crossref{https://doi.org/10.1134/S1560354708040102 }
\mathscinet{http://www.ams.org/mathscinet-getitem?mr=2456929}
\zmath{https://zbmath.org/?q=an:1229.37082}

Варианты соединения:

  • https://www.mathnet.ru/rus/rcd584
  • https://www.mathnet.ru/rus/rcd/v13/i4/p369

    • Эта публикация цитируется в следующих статьях:

    1. А. В. Болсинов, А. В. Борисов, И. С. Мамаев, “Геометризация теории Чаплыгина о приводящем множителе”, Нелинейная динам., 9:4 (2013), 627–640  
    2. Алексей В. Борисов, Николай А. Кудряшов, “Поль Пенлеве и его вклад в науку”, Регул. Хаотическая Дин., 19:1 (2014), 1–19    
    3. Алехандро Браво-Доддоли, Луис К. Гарсия-Наранхо, «Динамика сочлененного транспортного средства с $n$-прицепом», Regul. Chaotic Dyn., 20:5 (2015), 497–517        
    4. Алексей В. Борисов, Иван С. Мамаев, “Симметрии и редукция в неголономной механике”, Регул. Chaotic Dyn., 20:5 (2015), 553–604        
    5. И. А. Бизяев, В. В. Козлов, “Однородные системы с квадратичными интегралами, квазискобки Ли–Пуассона и метод Ковалевской”, Матем. Math., 206:12 (2015), 1682–1706              
    6. Алексей В. Борисов, Александр А. Килин, Иван С. Мамаев, “О задаче Адамара–Гамеля и динамике колесных транспортных средств”, Регул. Chaotic Dyn., 20:6 (2015), 752–766        
    7. Иван А. Бизяев, Алексей В. Борисов, Иван С. Мамаев, “Хоймановская конструкция и гамильтонизация неголономных систем”, СИГМА, 12 (2016), 012, 19 с.    
    8. Алексей В. Борисов, Сергей П. Кузнецов, “Правильное и хаотическое движение саней Чаплыгина при периодических импульсных моментных воздействиях”, Регул. Хаотическая динамика, 21:7-8 (2016), 792–803    
    9. И. А. Бизяев, А. В. Борисов, И. С. Мамаев, “Динамика саней Чаплыгина на цилиндре”, Регул. Chaotic Dyn., 21:1 (2016), 136–146          
    10. Яап Элдеринг, “Реализация неголономной динамики как предела сил трения”, Regul. Chaotic Dyn., 21:4 (2016), 390–409    
    11. А. В. Борисов, И. С. Мамаев, И. А. Бизяев, “Историко-критический обзор развития неголономной механики: классический период”, Нелинейная динам., 12:3 (2016), 385–411        
    12. А. В. Борисов, А. А. Килин, И. С. Мамаев, “О проблеме АдамараГамеля и динамике колесных экосистем”, Нелинейная динам., 12:1 (2016), 145–163  
    13. Алексей В. Борисов, Иван С. Мамаев, Иван А. Бизяев, “Историко-критический обзор развития неголономной механики: классический период”, Регул. Chaotic Dyn., 21:4 (2016), 455–476    
    14. Иван А. Бизяев, “Инерционное движение роллера ”, Регул. Хаотическая динамика, 22:3 (2017), 239–247      
    15. Алексей В. Борисов, Иван С. Мамаев, “Неоднородные сани Чаплыгина”, Регул. Chaotic Dyn., 22:4 (2017), 435–447      
    16. Иван А. Бизяев, Алексей В. Борисов, Иван С. Мамаев, “Сани Чаплыгина с параметрическим возбуждением: хаотическая динамика и неголономное ускорение”, Регул. Chaotic Dyn., 22:8 (2017), 955–975    
    17. А. В. Борисов, И. С. Мамаев, “Неоднородные сани Чаплыгина”, Нелинейная динам., 13:4 (2017), 625–639        
    18. А. В. Борисов, И. С. Мамаев, И. А. Бизяев, “Динамические системы с неинтегрируемыми связями, вакономная механика, субриманова геометрия и неголономная механика”, Изв. Опросы, 72:5 (2017), 783–840              
    19. С. n$”, Рус. Дж. Нонлин. Дин., 15:4 (2019), 457–475      
    20. Андрей В. Цыганов, “Гамильтонизация и разделение переменных для шара Чаплыгина на вращающейся плоскости”, Регул. Chaotic Dyn., 24:2 (2019), 171–186    
    21. Александр А. Килин, Елена Н. Пивоварова, “Качественный анализ неголономного качения резинового колеса с острыми кромками”, Регул. Chaotic Dyn., 24:2 (2019), 212–233    
    22. Андрей А. Ардентов, Юрий Л. Караваев, Кирилл С. Ефремов, “Эйлеровы эластики для оптимального управления движением мобильных колесных роботов: проблема экспериментальной реализации”, Регул. Хаотическая динамика, 24:3 (2019), 312–328    
    23. Иван А. Бизяев, Алексей В. Борисов, Иван С. Мамаев, “Различные модели качения робота-шара по плоскости как обобщение задачи о шаре Чаплыгина”, Регул. Chaotic Dyn., 24:5 (2019), 560–582      
    24. Курт М. Элерс, Яир Койллер, «Картан встречается с Чаплыгиным», Теор. заявл. мех., 46:1 (2019), 15–46    
    25. Луис К. Гарсия-Наранхо, “Гамильтонизация, сохранение меры и первые интегралы многомерной резиновой сферы Рауса”, Теор. заявл. мех., 46:1 (2019), 65–88    
    26. Бизяев И.А. Борисов А.В. Мамаев И.С., “Динамика саней Чаплыгина с неуравновешенным ротором: регулярное и хаотическое движение”, Нелинейная динамика, 98:3 (2019), 2277–2291          
    27. Бизяев И.А. Борисов В.А. Козлов В.В. Мамаев И.С., “Фермиподобное ускорение и степенной рост энергии в неголономных системах”, Нелинейность, 32:9 (2019), 3209–3233          
    28. Фассо Ф., Гарсия-Наранхо Л.К., Монтальди Дж., “Интегрируемость и динамика N-мерной симметричной ТОР Веселовой”, J. Nonlinear Sci., 29:3 (2019), 1205–1246          
    29. Гарсия-Наранхо Л.К., “Обобщение теоремы Чаплыгина о редуцирующих множителях с применением к многомерной неголономной динамике”, J. Phys. А-Математика. Теор., 52:20 (2019), 205203        
    30. Йона Т., Ор Ю., «Модель колесной трехзвенной змеи: особенности в неголономных ограничениях и гибридной прерывистой динамике, вызванной кулоновским трением», Nonlinear Dyn. , 95:3 (2019), 2307–2324        
    31. Федонюк В. Таллапрагада, к.х.н., “Хаотическая динамика саней Чаплыгина с пассивным внутренним ротором”, Нелинейная динамика, 95:1 (2019), 309–320        
    32. Бизяев И.А. Борисов А.В. Кузнецов С.П., “Сани Чаплыгина с трением, движущиеся за счет периодических колебаний внутренней массы”, Нелинейная динамика, 95:1 (2019), 699–714      
    33. Иван С. Мамаев, Евгений В. Ветчанин, “Динамика резиновой сферы Чаплыгина при периодическом контроле”, Регул. Chaotic Dyn., 25:2 (2020), 215–236    
    34. Эмам С.А., “Обобщенные уравнения Лагранжа для систем с общими ограничениями и распределенными параметрами”, Сист. Дин., 49:1 (2020), 95–117          
    35. Сато Н., “Статистическая механика с неинтегрируемыми топологическими ограничениями: самоорганизация в заузленном фазовом пространстве”, Фундамент. Phys., 61:10 (2020), 103304          
    36. Сансонетто Н. Зоппелло М. , “О формировании траектории гидродинамических саней Чаплыгина”, IEEE Control Syst. Lett., 4:4 (2020), 922–927        
    37. Карапетян В. А., Шишков А. А., “Динамика конька Чаплыгина на горизонтальной плоскости при анизотропном сухом трении”, Изв. ун-т мех. Бык., 75:2 (2020), 47–49.
    38. Гарсия-Наранхо Л.К., Марреро Дж.К., “Возвращение к геометрии неголономных систем Чаплыгина”, Нелинейность, 33:3 (2020), 1297–1341          
    39. Шамин А.Ю., “Динамика саней Чаплыгина на горизонтальной плоскости с трением”, Моск. ун-т мех. Bull., 75:1 (2020), 13–20          
    40. Валерий В. Козлов, «Интегралы систем кровообращения квадратичных в Моменте», Регул. Chaotic Dyn., 26:6 (2021), 647–657      
    41. Дж. Сюн, Ю.-Б. Цзя, К. Лю, “Симметрия и относительные равновесия велосипедной системы”, Рус. Дж. Нонлин. Динамика, 17:4 (2021), 391–411    
    42. Гарсия-Наранхо L.U.I.S.C. Vermeeren M.A.T.S., “Сохраняющая структуру дискретизация репараметризованных во времени гамильтоновых систем с применением к неголономной механике”, J. Comput. Dynam., 8:3 (2021), 241–271        
    43. Могхаддам Б.М., Чабра Р., «Наведение, навигация и управление космическими роботизированными полетами на орбите: обзор и перспективное видение», Acta Astronaut., 184 (2021), 70–100      
    44. Мюллер А., “О коэффициентах Гамеля и уравнениях Больцмана-Гамеля для твердого тела”, J. Nonlinear Sci., 31:2 (2021), 40        
    45. Бальсейро П. Япу Л.П., “Сохраняющиеся величины и гамильтонизация неголономных систем”, Ann. Инст. Анри Пуанкаре-Аналь. Non Lineaire, 38:1 (2021), 23–60        
    46. Бизяев И. Болотин С. Мамаев И., “Нормальные формы и усреднение в задаче об ускорении в неголономной механике”, Хаос, 31:1 (2021), 013132        
    47. А. Ю. Шамин. О движении саней Чаплыгина по Горизонтальная плоскость с трением в асимметричном случае”, рус. Дж. Нонлин. Динамика, 18:2 (2022), 243–251    

    Ссылки на статьи в Google Scholar: русские цитаты, английские цитаты
    Статьи по теме в Google Scholar: русские статьи, Английские статьи

    QR-?

    Динамика резиновой сферы Чаплыгина при периодическом контроле

    1. «>

      Ардентов А. А., Караваев Ю. Л., Ефремов К. С. Эластика Эйлера для оптимального управления движением мобильных колесных роботов: проблема экспериментальной реализации, Regul. Хаотичный дин. , 2019, том. 24, нет. 3, стр. 312–328.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    2. Арнольд В.И., Обыкновенные дифференциальные уравнения , Берлин: Springer, 2006.

      Google ученый

    3. Артемова Е. М., Килин А. А. Интегрируемый случай в динамике трехзвенного автомобиля // Междунар. конф. «Нелинейность, информация и робототехника» (Иннополис, Россия, 2020), подана.

      Google ученый

    4. Артемова Е.М., Килин А.А. Динамика и управление трехзвенной колесной машиной // Междунар. конф. «Нелинейность, информация и робототехника» (Иннополис, Россия, 2020), подана.

      Google ученый

    5. Бизяев И. А. Движение роллера по инерции // Регул. Хаотичный дин. , 2017, том. 22, нет. 3, стр. 239–247.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    6. Бизяев И. А., Борисов А. В., Кузнецов С. П. Сани Чаплыгина с периодически колеблющейся внутренней массой // Europhys. лат. , 2017, том. 119, нет. 6, 60008, 7 стр.

      Google ученый

    7. Бизяев И. А., Борисов А. В., Кузнецов С. П. Сани Чаплыгина с трением, движущимся за счет периодических колебаний внутренней массы // . Нелинейная динамика. , 2019, том. 95, нет. 1, стр. 699–714.

      Артикул Google ученый

    8. Бизяев И. А., Борисов А. В., Мамаев И. С. Различные модели качения робота-шара по плоскости как обобщение задачи о шаре Чаплыгина, Регул. Хаотичный дин. , 2019, том. 24, нет. 5, стр. 560–582.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    9. Бизяев И. А., Борисов А. В., Мамаев И. С. Экзотическая динамика неголономного роликохода с периодическим управлением // Regul. Хаотичный дин. , 2018, т. 1, с. 23, вып. 7–8, стр. 983–994.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    10. Bohl, P., Über ein in der Theorie der säkularen Störungen vorkommendes Problem, J. Reine Angew. Мат. , 1909, т. 1, с. 135, стр. 189–203.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    11. Болотин С. В. Задача оптимального управления шаром Чаплыгина внутренними роторами, Regul. Хаотичный дин. , 2012, том. 17, нет. 6, стр. 559–570.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    12. «>

      Борисов А.В., Иванова Т.Б., Караваев Ю.В. Л., Мамаев И. С., Теоретические и экспериментальные исследования качения шара на вращающейся плоскости (поворотный стол), Eur. Дж. Физ. , 2018, т. 1, с. 39, нет. 6, 065001, 13 стр.

      Google ученый

    13. Борисов А.В., Килин А.А., Караваев Ю.В. Л., Клековкин А.В. Стабилизация движения сферического робота с помощью обратных связей. Мат. Модель. , 2019, том. 69, стр. 583–592.

      Артикул MathSciNet Google ученый

    14. Борисов А.В., Мамаев И.С., Бизяев И.А. Историко-критический обзор развития неголономной механики: классический период, Regul. Хаотичный дин. , 2016, том. 21, нет. 4, стр. 455–476.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    15. Борисов А.В., Мамаев И.С., Бизяев И. А. Иерархия динамики качения твердого тела без проскальзывания и кручения на плоскости и сфере, Regul. Хаотичный дин. , 2013, том. 18, нет. 3, стр. 277–328.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    16. Бу-Раби, Н. М., Марсден, Дж. Э., и Ромеро, Л. А., Геометрическая обработка яйца Джеллета, ZAMM Z. Angew. Мат. мех. , 2005, том. 85, нет. 9, стр. 618–642.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    17. Браво-Доддоли, А. и Гарсия-Наранхо, Л. К., Динамика сочлененного n — прицепа, Regul. Хаотичный дин. , 2015, том. 20, нет. 5, стр. 497–517.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    18. Броер Х. и Симо К. Уравнение Хилла с квазипериодическим воздействием: языки резонанса, очаги нестабильности и глобальные явления, стр. бол. соц. Бразилия. Мат. (NS) , 1998, vol. 29, нет. 2, стр. 253–293.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    19. Чаплыгин С.А. К теории движения неголономных систем. Теорема о уменьшающем множителе, Regul. Хаотичный дин. , 2008, том. 13, нет. 4, стр. 369–376; см. также: Мат. сб. , 1912, том. 28, нет. 2, стр. 303–314.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    20. Дарвин, Г. Х., VIII. О влиянии геологических изменений на ось вращения Земли, Philos. Транс. Р. Соц. Лонд. , 1877, т. 1, с. 167, стр. 271–312.

      Google ученый

    21. Федоров Ю.В. Н. и Гарсия-Наранхо, Л. С., Гидродинамические сани Чаплыгина, J. Phys. А , 2010, вып. 43, нет. 43, 434013, 18 стр.

      Google ученый

    22. «>

      Фейгенбаум, М. Дж., Количественная универсальность для класса нелинейных преобразований, J. Stat. физ. , 1978, том. 19, нет. 1, стр. 25–52.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    23. Гонченко А. С., Гонченко С. В., Казаков А. О. Богатство хаотической динамики в неголономной модели кельтского камня, Regul. Хаотичный дин. , 2013, том. 18, нет. 5, стр. 521–538.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    24. Гонченко А.С., Гонченко С.В., Казаков А.О., Самылина Е.А. Хаотическая динамика и мультистабильность в неголономной модели кельтского камня. . Радиофиз. Квантовый Эл. , 2019, том. 61, нет. 10, стр. 773–786; см. также: Изв. Выш. Учебн. Завед. Радиофизика , 2018, т. 1, с. 61, нет. 10, стр. 867–882.

      Артикул Google ученый

    25. «>

      Хайрер Э., Любич Ч. и Ваннер Г., Геометрическое численное интегрирование: алгоритмы сохранения структуры для обыкновенных дифференциальных уравнений , Springer Ser. вычисл. Матем., вып. 31. New York: Springer, 2006.

    26. Иванова Т.Б., Килин А.А., Пивоварова Е.Н. Управляемое движение сферического робота маятникового типа по наклонной плоскости. Докл. физ. , 2018, т. 1, с. 63, нет. 7, стр. 302–306; см. также: Докл. акад. Наук , 2018, том. 481, нет. 3, стр. 258–263.

      Артикул Google ученый

    27. Иванова Т.Б., Килин А.А., Пивоварова Е.Н. Управляемое движение сферического робота с обратной связью: 1, Ж. динам. Система управления , 2018, т. 1, с. 24, нет. 3, стр. 497–510.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    28. Ильин К. И., Моффат Х. К., Владимиров В. А. Динамика катящегося робота, Проц. Натл. акад. науч. США , 2017, том. 114, нет. 49, стр. 12858–12863.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    29. Джорба, А., Симо, К., О приводимости линейных дифференциальных уравнений с квазипериодическими коэффициентами, Дж. Дифференциальные уравнения , 1992, том. 98, нет. 1, стр. 111–124.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    30. Камке, Э., Differentialgleichungen. Lösungsmethoden und Lösungen: Vol. 1. Gewöhnliche Differential-gleichungen , 9-е изд., Штутгарт: Teubner, 1977.

      Книга МАТЕМАТИКА Google ученый

    31. Канеко К., Удвоение тора, Progr. Теор. физ. , 1983, том. 69, нет. 6, стр. 1806–1810.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    32. «>

      Канеко К., Колебание и удвоение тора, Progr. Теор. физ. , 1984, том. 72, нет. 2, стр. 202–215.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    33. Караваев Ю.В. Л., Килин А.А. Неголономная динамика и управление сферическим роботом с внутренней омниколесной платформой: теория и эксперименты, Proc. Стеклова Мат. , 2016, том. 295, стр. 158–167; см. также: Тр. Мат. Инст. Стеклова , 2016, т. 1, с. 295, стр. 174–183.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    34. Казаков А. О. О возникновении смешанной динамики в результате столкновения странных аттракторов и репеллеров в обратимых системах, Радиофиз. Квантовый Эл. , 2019, том. 61, вып. 8–9, стр. 650–658; см. также: Изв. Выш. Учебн. Завед. Радиофизика , 2018, т. 1, с. 61, вып. 8–9, стр. 729.–738.

      Артикул Google ученый

    35. «>

      Килин А. А., Пивоварова Е. Н. Волчок Чаплыгина с периодическим гиростатическим моментом // рус. Дж. Матем. физ. , 2018, т. 1, с. 25, нет. 4, стр. 509–524.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    36. Килин А. А., Пивоварова Е. Н. Качение усеченного шара без проскальзывания и вращения по плоскости, 9.0143 Регул. Хаотичный дин. , 2017, том. 22, нет. 3, стр. 298–317.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    37. Килин А. А., Пивоварова Е. Н. Качественный анализ неголономного качения резинового колеса с острыми кромками // Регул. Хаотичный дин. , 2019, том. 24, нет. 2, стр. 212–233.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    38. Козлов В.В., Методы качественного анализа в динамике твердого тела , Москва-Ижевск: НИЦ Динамика, ИВТ, 2000.

      МАТЕМАТИКА Google ученый

    39. Кулешов А.С. Дальнейшее развитие математической модели снейкборда, Регул. Хаотичный дин. , 2007, том. 12, нет. 3, стр. 321–334.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    40. Кулешов А.С. Математическая модель скейтборда с одной степенью свободы // Докл. физ. , 2007, том. 52, нет. 5, стр. 283–286; см. также: Докл. акад. Наук , 2007, т. 1, с. 414, нет. 3, стр. 330–333.

      Артикул МАТЕМАТИКА Google ученый

    41. Кузнецов С.П. Влияние периодического внешнего возмущения на систему, демонстрирующую переход порядок-хаос через период, Письма в ЖЭТФ. , 1984, том. 39, нет. 3, стр. 133–136; см. также: Письма в Ж. Экспер. Теорет. Физ. , 1984, том. 39, нет. 3, стр. 113–116.

      Google ученый

    42. Кузнецов С.П. Регулярная и хаотическая динамика саней Чаплыгина при периодическом переключении неголономной связи // Регул. Хаотичный дин. , 2018, т. 1, с. 23, нет. 2, стр. 178–192.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    43. Кузнецов С., Фейдель Ю. и Пиковский А. Ренормализационная группа для масштабирования в конечной точке удвоения тора, Phys. Ред. E , 1998, том. 57, нет. 2, стр. 1585–1590.

      Артикул MathSciNet Google ученый

    44. Лерман Л.М., Тураев Д.В. Нарушение симметрии в обратимых системах. Регул. Хаотичный дин. , 2012, том. 17, вып. 3–4, стр. 318–336.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    45. «>

      Маркеев А. П. Интегрируемость задачи о качении сферы с многосвязной полостью, заполненной идеальной жидкостью, Изв. акад. наук СССР. мех. Тверь. Тела , 1986, вып. 21, нет. 1. С. 64–65 (рус.).

      Google ученый

    46. Маркеев А.П., Динамика твердого тела, сталкивающегося с твердой поверхностью , Ижевск: НИЦ Динамика ИВТ, 2014.

      Google ученый

    47. Мартыненко Ю.В. G., Управление движением мобильных колесных роботов, J. Math. науч. (Нью-Йорк) , 2007, том. 147, нет. 2, стр. 6569–6606; см. также: Фундамент. прикл. Мат. , 2005, том. 11, нет. 8, стр. 29–80.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    48. Моринага А., Свинин М. и Ямамото М., Стратегия планирования движения сферического катящегося робота, приводимого в движение двумя внутренними роторами, IEEE Trans. по робототехнике , 2014, вып. 30, нет. 4, стр. 993–1002.

      Артикул Google ученый

    49. Москвин А. Ю. Шар Чаплыгина с гиростатом: сингулярные решения, Нелин. Динам. , 2009, том. 5, нет. 3. С. 345–356.

      Артикул Google ученый

    50. Москвин А. Ю., Резиновый шарик на плоскости: сингулярные решения, Нелин. Динам. , 2010, том. 6, нет. 2. С. 345–358.

      Артикул Google ученый

    51. Мюррей, Р. М. и Састри, С. Ш., Планирование неголономного движения: управление с помощью синусоид, IEEE Trans. Автомат. Контроль , 1993, вып. 38, нет. 5, стр. 700–716.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    52. Неймарк Ю.А. I., О некоторых случаях зависимости периодических движений от параметров, Докл. акад. Наук СССР, 1959, вып. 129, нет. 4. С. 736–739 (рус.).

      MathSciNet Google ученый

    53. Неймарк, Ю. И., Фуфаев Н.А., Динамика неголономных систем , Пер. Мат. Моногр., т. 2, с. 33, Провиденс, Род-Айленд: AMS, 1972.

      МАТЕМАТИКА Google ученый

    54. Поллард Б., Федонюк В., Таллапрагада П., Плавание по предельным циклам с неголономными ограничениями, Нелинейный динам. , 2019, том. 97, нет. 4, стр. 2453–2468.

      Артикул МАТЕМАТИКА Google ученый

    55. Поллард, Б. и Таллапрагада, П., Пассивные придатки улучшают маневренность рыбоподобных роботов, IEEE/ASME Trans. Мехатроника , 2019, вып. 24, нет. 4, стр. 1586–1596.

      Артикул Google ученый

    56. «>

      Путкарадзе В. и Роджерс С., О динамике катящегося шара, приводимого в движение внутренними точечными массами, Meccanica , 2018, том. 53, нет. 15, стр. 3839–3868.

      Артикул MathSciNet Google ученый

    57. Раух-Войцеховски, С. и Пшибыльска, М., О динамике желейного яйца. Новый взгляд на асимптотические решения, Regul. Хаотичный дин. , 2020, том. 25, нет. 1, стр. 40–58.

      Артикул MathSciNet Google ученый

    58. Сакер, Р., Об инвариантных поверхностях и бифуркации периодических решений обыкновенных дифференциальных уравнений, Отчет IMM-NYU 333, Нью-Йоркский университет, 1964.

      Google ученый

    59. Шен Дж., Шнайдер Д. А. и Блох А. М. Управляемость и планирование движения многотельной сферы Чаплыгина и волчка Чаплыгина, Междунар. J. Устойчивое нелинейное управление , 2008, т. 1, с. 18, нет. 9, стр. 905–945.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    60. Тафриши С. А., Эсмаилзаде Э., Свинин М. и Ямамото М. Гидравлический приводной механизм для вращающихся роботов, в Проц. IEEE 4-й междунар. конф. по передовой робототехнике и мехатронике (ICARM, 2019), стр. 256–261.

      Google ученый

    61. Тилбери, Д., Мюррей, Р., и Састри, С., Генерация траектории для задачи N -Trailer с использованием нормальной формы Гурса, IEEE Trans. Автомат. Контроль , 1995, вып. 40, нет. 5, стр. 802–819.

      Артикул MathSciNet МАТЕМАТИКА Google ученый

    62. Тиссеран, Ф., Tra i té de la Mécanique Céleste: Vol. 2. Теория фигур небесных тел и движения вращения , Париж: Gauthier-Villars, 1891.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *